lunes, 29 de julio de 2019
Juegos Olimpicos
Haz Clic Aqui para ver las diferentes disciplinas deportivas que hay. Haz una guia de 5 preguntas de 15 disciplinas de tu elección. Aqui tambien te puedes guiar para sacar tus preguntas acerca de tales disciplinas.Y aqui hay mas. Tambien aqui
Funciones
¡Saludos! aqui les dejo un video para que aprendan un poco a manera superficial lo que son funciones.
domingo, 28 de julio de 2019
Inecuaciones de 2 variables
Geometria
¡Saludos! aqui les dejo un enlace de un libro de geometria busquen el cap. 4. Para descargar Haz Clic Aqui
Suma y resta de Fracciones Algebraicas
¡Saludos! en este articulo veremos como resolver problemas de adición(suma) y sustracción(resta) de Fracciones algebraicas, como siempre les dejo un enlace a material complementario para reforzar conocimientos y despejar dudas (Clic Aqui).
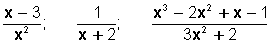
Las fracciones algebraicas tienen un comportamiento similar a las fracciones numéricas.
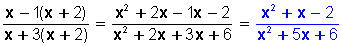
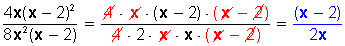
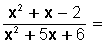
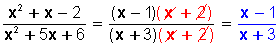
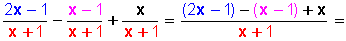
Como el denominador es común (x + 1) , este se ha unificado en una sola fracción, que ahora tiene como numerador a todas las cantidades que eran numeradores en las fracciones que estamos sumando y restando. Nótese que dichas cantidades se anotan entre paréntesis cuando no son monomios, para no confundir luego los signos.
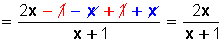
Hicimos las operaciones posibles y llegamos al resultado.
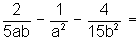
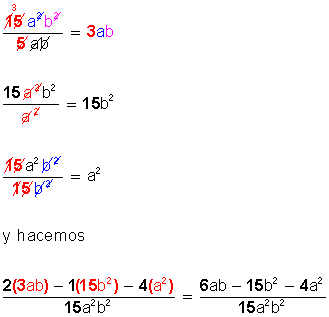
Esta es la forma tradicional de operar cuando hemos hallado el m.c.d. Pero también hay otra, como la siguiente:
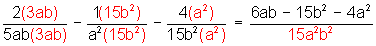
Nótese que “los términos que faltan” se obtienen haciendo la misma división del caso anterior.
El m.c.m. de los denominadores, o mínimo común denominador (m.c.d.) es x(x − 3)
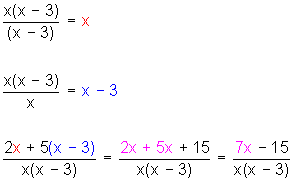
Una fracción algebraica es una expresión fraccionaria en la que numerador y denominador son polinomios.
Son fracciones algebraicas:
Las fracciones algebraicas tienen un comportamiento similar a las fracciones numéricas.
El valor de una fracción no se altera si se multiplican o dividen el numerador y denominador por una misma cantidad. Esta cantidad debe ser distinta de cero.
Por ejemplo:
Si 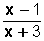 se multiplica por x + 2 en su numerador y denominador resulta:
se multiplica por x + 2 en su numerador y denominador resulta:
Se recomienda hacer las operaciones con calma y mucha concentración ya que son frecuentes los errores de signos y los errores en el uso incorrecto de paréntesis.
Operaciones con fracciones algebraicas
Simplificar fracciones algebraicas
La simplificación de fracciones algebraicas es objeto de frecuentes errores, pero se simplifican igual que las fracciones ordinarias: dividiendo el numerador y el denominador por factores comunes. Entonces, la clave está en el factor común. Para simplificar al máximo habrá que factorizar los polinomios numerador y denominador.
Por ejemplo, simplificar:
Otro ejemplo, simplificar la fracción
Primero, factorizamos los polinomios del numerador y del denominador, para quedar
Como vemos, simplificar (o reducir) una fracción algebraica consiste en transformarla a otra equivalente cuya particularidad es ser irreductible (se puede simplificar sólo hasta un cierto nivel).
Suma y resta de fracciones algebraicas
Para sumar y restar procederemos de forma similar a como lo hacemos con fracciones de números enteros, reduciendo primero a común denominador .
Igual como ocurre con las fracciones de números enteros, la suma y resta de fracciones algebraicas puede ser con fracciones de igual denominador o de distinto denominador.
Suma y resta de fracciones algebraicas con igual denominador
Veamos el siguiente ejemplo de suma y resta:
Como el denominador es común (x + 1) , este se ha unificado en una sola fracción, que ahora tiene como numerador a todas las cantidades que eran numeradores en las fracciones que estamos sumando y restando. Nótese que dichas cantidades se anotan entre paréntesis cuando no son monomios, para no confundir luego los signos.
Ahora sacamos los paréntesis teniendo cuidado de cambiar el signo interior cuando delante del paréntesis hay un signo menos (−), y nos queda
Hicimos las operaciones posibles y llegamos al resultado.
Suma y resta de fracciones algebraicas con distinto denominador
Veamos el siguiente ejemplo:
Tal como lo hacíamos al sumar o restar fracciones de números enteros, utilizando el mínimo común múltiplo (m.c.m.) las fracciones con distintos denominadores se transforman en fracciones equivalentes con denominador común.
Entonces, que debemos hacer: encontrar el m.c.m . de los denominadores, que llamaremos mínimo común denominador (m.c.d.) . (No confundir con M.C.D, Máximo Común Divisor)
Para calcular el m.c.m. factorizamos
| 5ab | a 2 | 15b 2 | ÷ | a |
| 5b | a | 15b 2 | ÷ | a |
| 5b | 1 | 15b 2 | ÷ | b |
| 5 | 1 | 15b | ÷ | b |
| 5 | 1 | 15 | ÷ | 5 |
| 1 | 1 | 3 | ÷ | 3 |
| 1 | 1 | 1 |
Multiplicamos los factores y queda a • a • b • b • 5 • 3 = a 2 • b 2 • 15 que es lo mismo que 15a 2 b 2 y es el mínimo común denominador (m.c.d.) de las tres fracciones involucradas.
Conocido el m.c.d. operamos con fracciones con denominador común:
Previamente, dividimos el denominador común (15a 2 b 2 ) por cada uno de los denominadores individuales, para conocer la cifra o valor que se multiplica por cada uno de los numeradores, y lo hacemos así:
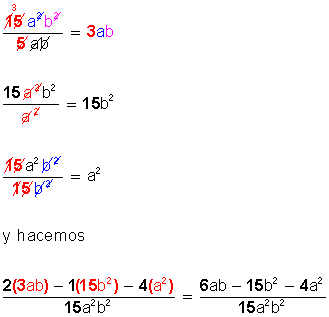
Esta es la forma tradicional de operar cuando hemos hallado el m.c.d. Pero también hay otra, como la siguiente:
Encontrado el m.c.d. (15a 2 b 2 ) se multiplica cada fracción (tanto numerador como denominador) por los términos que faltan por completar dicho m.c.d., del modo siguiente:
Nótese que “los términos que faltan” se obtienen haciendo la misma división del caso anterior.
Un ejemplo más:
Sumar 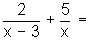
El m.c.m. de los denominadores, o mínimo común denominador (m.c.d.) es x(x − 3)
Hacemos
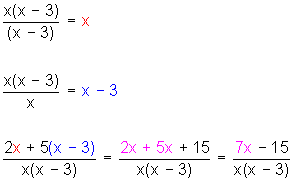
¿Qué hicimos? Sumamos los numeradores dejando el mismo denominador y simplificamos el numerador.
Desarrollar problemas de practica asignados en clase ingresando al siguiente enlace:
Regla de tres
¡Saludos! La regla de tres recibe su nombre porque al conocer 3 datos podemos hallar el resultado (Incógnita o valor desconocido). existen varios métodos para resolver, nosotros usaremos el método llamado "Proporcionalidad simple".
Para poder usar este método, debemos seguir unos cuantos pasos como ser:
1. Agrupar los datos.
2. La multiplicación de hace cruzado.
3. El numero que quedó solo divide.
Aquí les dejo un videotutorial de la regla de tres, en el cual podrán reforzar lo aprendido en clase.
Aquí les dejo un enlace con ejercicios de la regla de tres para que puedan comprender aun mas y puedan practicar, luego de ver su desarrollo, les recomiendo que observen de donde y como sale cada dato, y analicen cada ejercicio. luego los intenten hacer sin ver, esto les ayudará a comprender mejor este tema.(Clic Aquí)
Ejemplo 1
Ejemplo 2
sábado, 27 de julio de 2019
Ecuacion punto pendiente
La fórmula Punto-Pendiente de la ecuación de la
recta
Se estudiarán rectas que no son paralelas al eje Y, con
pendiente m, y que pasan por un punto
P1(x1, y1) . Cualquier otro punto P
de la recta lo denominaremos P(x, y) .
La pendiente
de la recta que pasa por P1(x1,
y1) y P2(x2, y2) es
La ecuación Punto- Pendiente es: y – y1
= m(x – x1).
Ejemplo 1
Hallar la ecuación de la recta que
pasa por el punto (-4, 3) con pendiente –1. Solución: La ecuación punto- pendiente
es y – 3 =
-1(x – (-4)).
⇒ y - 3 = -x – 4. ⇒ y
= -x - 1
Problema 1
Halle la
ecuación de la recta que pasa por el punto (2, -3) con pendiente 2.
Problema 2
2
Respuesta: y =
Ejemplo 2
1 x - 10
Halle la
ecuación de la recta que pasa por los puntos(-4, 3) and (2, -5).
Solution:
m = y2 - y1
m = - 5 - (3) = - 8 = - 4
x2 - x1
2 - (-4) 6 3
3 3 3
Problema 3
Halle la
ecuación de la recta que pasa por:
a) (3, -5) and (-4, 6). b)
(1, -2) and (3, 2). c)
(-1, -2) and (-3, 2).
Ejemplo 4
Escriba la ecuación de la recta 4x + 2y + 1 = 0, en la forma
general y = mx + b, llamada a veces forma pendiente-intersección
 |
Solución:
Determinar si dos ecuaciones representan rectas
paralelas
Dos rectas
son paralelas si tienen la misma pendiente
Ejemplo 5
 |
Determine si 3x –2y =5 y -6x + 4y =25 son paralelas. Solucion: Hallando la pendiente de cada una de las rectas.
Como ambas
pendientes son iguales, las rectas son paralelas.
Problema 4
Determine si
4x –3y =7 y -12x + 9y =25 son paralelas.
Ejemplo 6
Halle la ecuación de la recta paralela a 2x + 3y = 8 que pasa por
(5, 4). Solución:
3
3
de tal recta.
Problema 5
Halle la
ecuación de la recta paralela a 4x - 3y = 24 y que pasa por (1, -2).
Rectas perpendiculares
Dos rectas son perpendiculares si sus pendientes son el negativo
recíproco, una de la
otra.
Ejemplo 7
2
Problema 6
Escriba cada ecuación en la forma y = mx + b, señalando la
pendiente, la pendiente de una recta perpendicular y su intersección con el eje
Y.
Ecuación
|
y = mx + b
|
Pendiente
m1
|
Perpendicular
Pendiente
m2
|
Intersección
(0,
b)
|
12x – 9y + 36 = 0
|
||||
14x – 7y + 21 = 0
|
||||
5y – 15 = 0
|
||||
2y + 1 = 0
|
Descarga el PDF
Multiplicacion y División de fracciones algebraicas
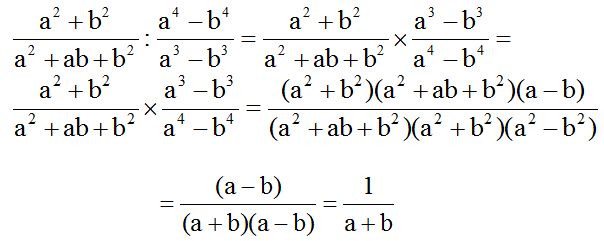
Saludos!!! Aqui les dejo le siguiente enlace para que puedan cocmplementar lo aprendido en clase
Clic Aqui. Otro enlace
He aqui otros recursos
Descargar este PDF
viernes, 26 de julio de 2019
Limites (Interpretacion de graficos)

¡Saludos!, en esta ocasión vamos a hacer una practica de interpretacion de graficas respecto a los limites. Por favor entren al siguiente enlace (Clic Aqui) en el cual podrán repasar un poco sobre los limites antes de comenzar con las interpretaciones de gráficas por si aun tienen alguna duda.
Para hacer una pequeña prueba de interpretacion de limites a partir de una grafica. Para ello haz Clic Aqui, y prueba tu capacidad de interpretación.
Aqui te dejo un video adicional para que entiendas mejor la interpretacion de limites.
Aqui otro video en el que aprenderemos a interpretar limites
aqui otro de ejemplo de limites infinitos.
A continuación les adjunto el enlacec al libro de matematicas aplicada a la administracion y la economia, no se asuste por la cantidad de temas que hay ahi, ud solo deberá de buscar la pagina No. 459 del libro y hacer los ejercicios de limites, si gusta dar un repaso del tema solo deberá ir a la No. 450 en donde se habla del tema.
Suscribirse a:
Comentarios (Atom)
Ejercicios de Derivadas
Aqui les dejo unos ejercicios de derivadas para que practiquen. Aqui un post donde aprenderan a utilizar la reglade la cadena Tabla d...
-
1 Dibuja un círculo con un compás. Coloca un lápiz en el compás. Ajusta la abertura del compás hasta que des con la medida apropiada para e...
-
Manual sobre la creación y edición de los archivos batch. Aprender a hacer nuestras propias aplicaciones copiando y pegando el código en e...